Thermal fluctuations in Rayleigh-Benard convection
Rayleigh-Benard Convection is usually considered in the context of a deterministic equation where the state of the system changes from a spatially uniform state ( conduction state ) to a state with spatial variations (convection state), when the temperature difference DT across the convection cell exceeds a critical value DTc . However, if the system includes a stochastic force, such as the inevitable thermal noise, then fluctuating convective flows (with zero mean and finite square mean amplitude) appear even below DTc. The amplitude of the fluctuations was predicted to become larger and eventually diverge as the system approaches the critical point in the absence of nonlinear saturation. Here, we present experimental measurements of the fluctuations below DTc in a large aspect ratio convection cell. These fluctions are observed using a spectral analysis enhanced shadow graph technique. Results of the fluctuation magnitude are confirmed by the existing theory.
For more information, see:
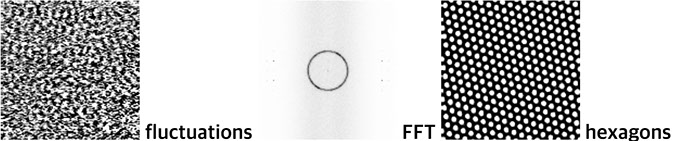
Above are shadow graph images for fluctuations, fluctuations in Fourier space, and hexagons.
Publications:
Mingming Wu, Guenter Ahlers, David C Cannell, Phys. Rev. Lett. vol. 75, 1743(1995).
Site created and maintained by Young Joon Suh

